Evolución de los Sistemas de Numeración y Codificación

A raíz de la necesidad de representar los caracteres de lenguas europeas distintas del inglés-americano, la difusión de la informática a culturas de raíz no latina puso rápidamente de manifiesto que 256 caracteres eran insuficientes para contener los grafos de todas las lenguas. Por ejemplo, el cirílico; el hebreo; el árabe; el griego, y el japonés por citar algunas. Se hizo evidente la necesidad un sistema con más de 256 posibilidades, lo que condujo a establecer sistemas de codificación en los que cada carácter ocupaba más de un octeto (al menos ciertos caracteres), razón por la cual a estos sistemas se les conoce genéricamente como de caracteres anchos.
La solución adoptada comprende dos grandes grupos: el sistema multibyte y el sistema de caracteres anchos ,de los que existen distintas variedades. Generalmente el primero se utiliza en representación externa (almacenamiento) y comunicaciones, mientras que el segundo es preferido para representaciones internas.

Tipos de Sistemas de Codificación y Numeración

Sistema multibyte

Si se trata de representar juegos de más de 256 caracteres en almacenamientos externos o en sistemas de transmisión, en los que es importante la economía de espacio y/o ancho de banda, la solución ha consistido en utilizar sistemas de codificación multibyte. Conocidos abreviadamente como MBCS ("Multibyte Character Set").
Como su nombre indica utilizan más de un octeto, pero la anchura de los distintos caracteres es variable según la necesidad del momento. Los caracteres multibyte son una amalgama de caracteres de uno y dos bytes de ancho que puede considerarse un superconjunto del ASCII de 8 bits. Por supuesto una convención de este tipo exige una serie de reglas que permitan el análisis ("Parsing") de una cadena de bytes para identificar cada carácter.

Existen distintas versiones de este tipo de codificación que se utilizan en distintas circunstancias:

· JIS ("Japanese Industrial Standar"). Es utilizado principalmente en comunicaciones, por ejemplo correo electrónico, porque utiliza solo 7 bits para cada carácter. Usa secuencias de escape para conmutar entre los modos de uno y dos bytes por carácter y para conmutar entre los diversos juegos de caracteres.

· Shift-JIS. Introducido por Microsoft y utilizado en el sistema MS-DOS, es el sistema que soporta menos caracteres. Cada byte debe ser analizado para ver si es un carácter o es el primero de un dúo.

· EUC ("Extended Unix Code"). Este sistema es utilizado como método de codificación interna en la mayoría de plataformas Unix. Acepta caracteres de más de dos bytes, por lo que es mucho más extensible que el Shift-JIS, y no está limitado a la codificación del idioma japonés. Resulta muy adecuado para el manejo de múltiples juegos de caracteres. UTF-8 ("Unico de transformation format"). En este sistema, cada carácter se representa mediante una secuencia de 1 a 4 bytes, aunque en realidad, el número de bits destinados a representar el carácter se limita a un máximo de 21 (el resto son metadatos -información sobre información). El objeto de estos metadatos es que la secuencia pueda ser interpretada a partir de cualquier posición. Es decir, que de la simple inspección de un trozo, sea posible conocer donde comienza cada carácter y cuantos bytes lo componen.

Sistema Binario

En matemáticas e informática, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Los ordenadores trabajan internamente con dos niveles de voltaje, por lo que su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).

Sistema Decimal

Es un sistema de numeración en el que las cantidades se representan utilizando como base el número diez, por lo que se compone de las cifras: cero (0); uno (1); dos (2); tres (3); cuatro (4); cinco (5); seis (6); siete (7); ocho (8) y nueve (9). Este conjunto de símbolos se denomina números árabes. los números decimales son lo que no tienen coma (,).

Sistema Octal

El sistema numérico en base 8 se llama octal y utiliza los dígitos 0 a 7.
Por ejemplo, el número binário para 74 (en decimal) es 1001010 (en binario), lo agruparíamos como 1 001 010. De modo que el número decimal 74 en octal es 112.
En informática, a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos. Sin embargo, para trabajar con bytes o conjuntos de ellos, asumiendo que un byte es una palabra de 8 bits, suele ser más cómodo el sistema hexadecimal, por cuanto todo byte así definido es completamente representable por dos dígitos hexadecimales.

Sistema Hexadecimal

A veces abreviado como hex, es el sistema de numeración posicional de base 16 —empleando por tanto 16 símbolos—. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria.

Conversión de los Sistemas de Numeración y Codificación

Binario a decimal

Para realizar la conversión de binario a decimal, realice lo siguiente:
Inicie por el lado derecho del número en binario, cada número multiplíquelo por 2 y elévelo a la potencia consecutiva (comenzando por la potencia 0).
Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.

Binario a decimal (Con decimal binario)

1. Inicie por el lado izquierdo, cada número multiplíquelo por 2 y elévelo a la potencia consecutiva a la inversa(comenzando por la potencia -1).
2.Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.

Decimal a binario

Se divide el número decimal entre 2 cuyo resultado entero se vuelve a dividir entre 2 y así sucesivamente. Una vez llegados al 1 indivisible se cuentan el último cociente, es decir el uno final (todo número binario excepto el 0 empieza por uno), seguido de los residuos de las divisiones subsiguientes. Del más reciente hasta el primero que resultó. Este número será el binario que buscamos. A continuación se puede ver un ejemplo con el número decimal 100 pasado a binario.

Otra forma de conversión consiste en un método parecido a la factorización en números primos. Es relativamente fácil dividir cualquier número entre 2. Este método consiste también en divisiones sucesivas. Dependiendo de si el número es par o impar, colocaremos un cero o un uno en la columna de la derecha. Si es impar, le restaremos uno y seguiremos dividiendo entre dos, hasta llegar a 1. Después sólo nos queda tomar el último resultado de la columna izquierda (que siempre será 1) y todos los de la columna de la derecha y ordenar los dígitos de abajo a arriba. Y luego se haría un cuadro con las potencias con el resultados.

Existe un último método denominado de distribución. Consiste en distribuir los unos necesarios entre las potencias sucesivas de 2 de modo que su suma resulte ser el número decimal a convertir. Sea por ejemplo el número 151, para el que se necesitarán las 8 primeras potencias de 2, ya que la siguiente, 28=256, es superior al número a convertir. Se comienza poniendo un 1 en 128, por lo que aún faltarán 23, 151-128=23, para llegar al 151. Este valor se conseguirá distribuyendo unos entre las potencias cuya suma den el resultado buscado y poniendo ceros en el resto. En el ejemplo resultan ser las potencias 4, 2, 1 y 0, esto es, 16, 4, 2 y 1, respectivamente.

Decimal (Con decimales) a binario

Inicie por el lado izquierdo, cada número multiplíquelo por 2 y si la parte entera queda mayor que 0 entonces en binario será 1 en caso contrario será 0
En caso de ser 1 para la siguiente división coja únicamente los decimales.
Después de realizar cada una de las multiplicaciones, coloque los números que ha obtenido en orden de aparición.
Hay que tener cuidado con este método pues algunos números tienen una representación infinita o muy larga, por ejemplo el 0.1

Ejemplos:

* 0.3125 (decimal) = 0.0101(binario). Proceso

0.3125*2 = 0.625 => 0
0.625*2 = 1.25 => 1
0.25*2 = 0.5 => 0
0.5*2 = 1 => 1
En orden: 0101

* 0.625 (decimal) = 0.101(binario). Proceso

0.625*2 = 1.25 => 1
0.25*2 = 0.5 => 0
0.5*2 = 1 => 1
En orden: 101

Binario a octal

Para realizar la conversión de binario a octal, realice lo siguiente:

1) Agrupe la cantidad binaria en grupos de 3 en 3 iniciando por el lado derecho. Si al terminar de agrupar no completa 3 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:

3) La cantidad correspondiente en octal se agrupa de izquierda a derecha.
Ejemplos:

* 110111 (binario) = 67 (octal). Proceso:

111 = 7

110 = 6

Agrupe de izquierda a derecha: 67

* 11001111 (binario) = 317 (octal). Proceso:

111 = 7

001 = 1

11 entonces agregue un cero, con lo que se obtiene 011 = 3

Agrupe de izquierda a derecha: 317

* 10000011 (binario) = 103 (octal). Proceso:

011 = 3

000 = 0

1 entonces agregue 001 = 1

Agrupe de izquierda a derecha: 103

Octal a binario

Cada dígito octal se lo convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.

Ejemplo:
247 (octal) = 010100111 (binario). El 2 en binario es 10, pero en binario de 3 bits es Oc(2) = B(010); el Oc(4) = B(100) y el Oc(7) = (111), luego el número en binario será 010100111

Binario a hexadecimal

Para realizar la conversión de binario a hexadecimal, realice lo siguiente:

1) Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:

3) La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.

Ejemplos:

* 10111010 (binario) = 1BA (hexadecimal). Proceso:

1010 = A
1011 = B
1 entonces agregue 0001 = 1
Agrupe de derecha a izquierda: 1BA

* 11011110101 (binario) = 6F5 (hexadecimal). Proceso:

0101 = 5
1111 = F
110 entonces agregue 0110 = 6
Agrupe de derecha a izquierda: 6F5

Hexadecimal a binario

Es Idéntico que para pasar de octal a binario, sólo que se remplaza por el equivalente de 4 bits, como de octal a binario.

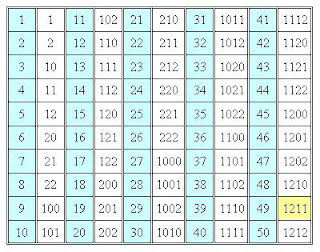
Tabla de Conversion Decimal,Binario, Hexadecimal y Octal